Heritability:

Summary of heritability equations for balanced and unbalanced datasets.
There are more ways to calculated H2 based on if you do spatial correction, gxe, and so on, but this is a start.

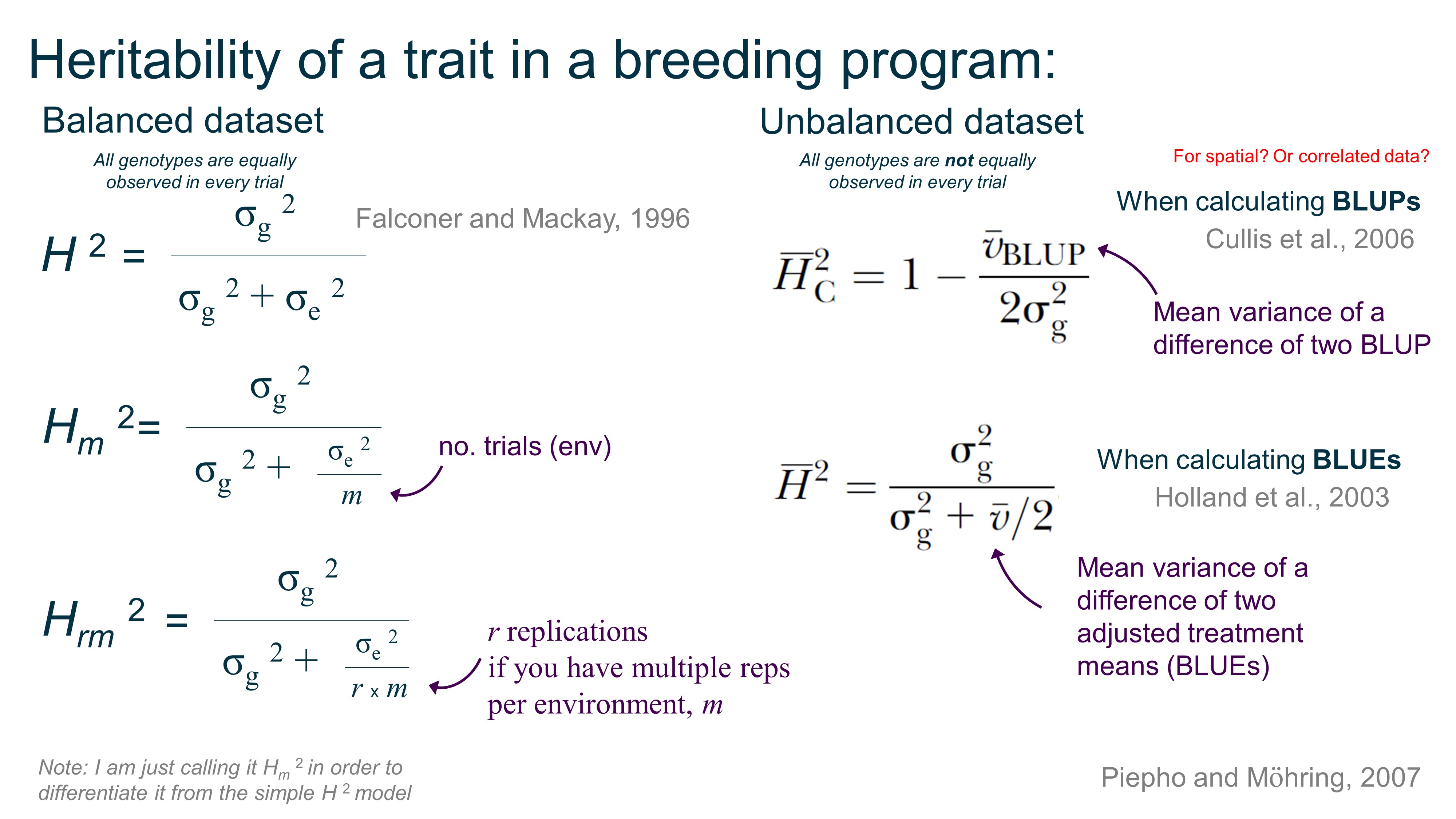
You can obtain σ g 2 (genotype variance) and σ e 2 (residual variance) in R using the lme4 package with VarCorr(model) after you’ve defined your model, but Dan Sweeney shared with me his function to calculate vBLUP:

  
library(lme4)
model1 <- lmer(Pheno~(1|genotypes)+Env+HD, data = EliteProgramData) 
S_1 <- as.data.frame(VarCorr(model1)); 
sigma2_g <- S_1[1,4]
sigma2_e <- S_1[2,4] #Assuming your model only has 1 random effect. If more than one, [2,4] becomes [n,4] where n = number of random effects + 1 

#Balanced H2
FalMac_H2 <- sigma2_g / (sigma2_g + sigma2_e)

m <- length(unique(EliteProgramData$Env))
MultiEnv_H2 <- sigma2_g / (sigma2_g + (sigma2_e/m))

#Unbalanced H2
Cullis_H2=function(model){
  library(arm)
  ses<- se.ranef(model)$'genotypes' #where 'm' is your model object from 'lmer' (replace 'genotypes' with whatever you call your individuals in the data)
  v_BLUP<- ses^2
  sigma2_g=VarCorr(model, comp="Variance")$'genotypes'[1]
  Reliability<- 1- v_BLUP/ (2\*sigma2_g)  #where sigma2_g is the genetic variance estimated with the model saved in 'm'
  H2<- round(mean(Reliability),3) #This is equivalent to broad-sense heritability on the line-mean (or family-mean, if your individuals are non-inbred families) basis
  H2
}

Cullis_H2(model1)